명목척도로 구성된 독립변수와 등간척도 이상으로 구성된 종속변수의 수가 각각 하나씩 있는 경우에 사용하는 분석입니다. 일원분산분석에는 두 개의 독립표본의 평균비교를 확장한 일원분산분석(One-Way ANOVA)과 Paired-diffefence test를 확장한 무작위 블록디자인의 일원분산분석으로 나눌 수 있습니다. 무작위 블록디자인에 의한 일원분산분석은 7.2에서 다루도록 하겠습니다.
예
속옷 회사에서 신체에 따른 기능성 속옷을 개발하기 위해 신체적 조건에 따른 신체만족도를 조사하기로 하였다. 신체적 조건에 따라 신체만족도에 차이가 있는지 알아보고자 한다.
1) 가설설정
분산분석에서 영가설은 각 집단별 종속변수의 평균값이 동일하다는 점입니다. 여기서는 집단이 여러 개이므로 다음과 같이 가설이 설정됩니다.
<연구가설> : 신체적 조건에 따라 신체만족도에 차이가 있다.
(영가설) : 
(대립가설) : 적어도 어느 두 집단은 다르다.
2) 유의수준 설정
3) 가정검토
분산분석을 적용하기 전에 조사자는 각 집단의 특성과 관련하여 다음과 같은 전제조건들이 충족되는지를 검토해야 합니다.
① 독립성 : 각 집단은 서로 독립적이어야 합니다.
② 정규성 : 각 집단을 정규분포를 이루어야 합니다.
③ 불편성 : 각 집단별 분산의 정도가 비슷해야 합니다.
4) 검정통계량
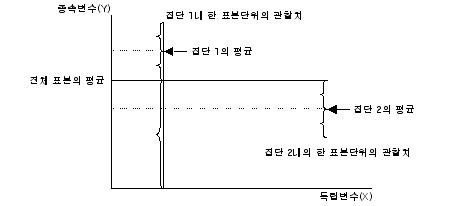
분산분석에서는 두 개 이상의 집단들의 평균값을 비교하기 위해 F값을 검정통계량으로 사용합니다. 조사자는 집단간의 차이를 구하기 위해 전체평균과 집단평균간의 차이와 집단평균과 개별관찰치와의 차이로 구분하여 계산합니다. 즉, (전체평균-개별관찰값) = (전체평균-집단평균)+(집단평균-개별관찰값)으로 계산합니다.
|
|
위 식의 각 구성요소를 제곱하면 세 가지 유형의 분산으로 구성됩니다.
|
|
+ |
|
= |
|
|
총변량(SST) |
+ |
집단간 변량(SSB) |
= |
집단내 변량(SSW) |
각 구성요소의 계산식에 대해 살펴봅시다.
① 총변량(SST : sum of squares total)은 각 관찰값들이 전체 표본의 평균들을 중심으로 얼마만큼 떨어져 있는가를 측정하는 것입니다.
: 종속변수 
의 개별관찰값
: 전체표본에서의 종속변수의 평균
: 집단
의 표본 수
: 집단의 수
② 집단간 변량(SSB : sum of squares between groups)은 독립변수에 의해 나누어진 각 집단의 평균이 전체표본 평균의 중심으로 얼마나 떨어져 있는가를 측정하는 것입니다.
번째 집단의 표본 수
번째 집단의 평균
③ 집단내 변량(SSW : sum of squares within groups)은 각 표본집단내 개별관찰치들이 각 표본집단의 평균을 중심으로 어느 정도 떨어져 있는가를 측정하는 것입니다.
집단간 변량과 집단내 변량이 구해지면 이를 통해 집단간의 차이를 검정할 수 있습니다. 분산분석에서는 집단간 차이가 유의하기 위해서는 집단내 변량은 가능한 적어야 하며 집단간 변량은 가능한 커야 합니다. 이를 위해 분산분석에서는 집단간 분산치와 집단내 분산치의 상대적인 비율을 나타내는 
통계량을 이용하여 집단간 차이에 대한 검정을 합니다.
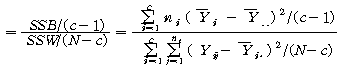
분산분석에서의 자유도는 크게 세 가지입니다.
집단간 변량의 자유도는 독립표본의 수 - 1(=
)이고, 집단내 변량의 자유도는 사례수 - 독립표본 수(=
), 총변량의 자유도는 사례수 - 1(=
)입니다.
이를 토대로 분산분석표를 작성해 본 후 분석해 봅시다.
|
Source |
제곱합 SS |
자유도 df |
제곱평균 MS |
F |
|
집단간 변량 |
|
|
|
|
|
|
|
|
|
|
|
집단내 변량 |
|
|
|
|
|
총변량 |
|
|
|
|
조사자는 집단간 차이에 대한 가설설정을 위해 
의 임계치를 구해야 합니다. 
의 임계치는 유의수준과 각각의 자유도에 따라 결정이 됩니다. 만약 계산된 
값이 
의 임계치 (=
)값보다 작으면, 영가설을 채택하게 됩니다. 반대로 
값이 
의 임계치 (=
)값보다 크면, 영가설을 기각하고 집단간 차이가 있다고 결론지을 수 있습니다.
5) 실행방법
일원분산분석을 시작하기 위해 [예제 09-1]파일을 열어봅니다. 파일을 열면 데이터 편집기에 6개의 변수가 있습니다. 2장에서 변수변환에 대해 배운 적이 있지요? 여기서는 5개의 변수를 신체만족도라는 하나의 변수로 합치려고 합니다. 2장을 배운 내용을 토대로 간단히 설명을 하겠습니다.
우선 변수변환을 위해 변환메뉴에 들어가서 변수계산을 클릭해 줍니다. 키, 몸무게, 가슴둘레, 허리둘레, 힙둘레의 변수는 모두 각각에 대한 자신의 만족도를 측정한 것입니다. 이에 대한 만족도를 하나의 신체만족도로 만들어주기 위해 다섯 개의 변수를 합한 후 그 값을 변수의 개수로 나누어줍니다.
|
변환(T)→변수계산(C) |
이 절차를 따라 하면 [그림 7.1]과 같은 대화상자가 나타납니다.
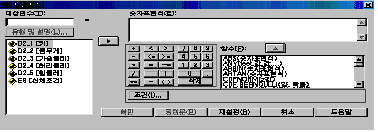
대상변수에는 새로 생성할 변수명을 적어 넣습니다. 여기서는 신체만족도에 관한 내용을 적으면 되지만 글자수는 한글인 경우 4자, 영문인 경우 8자로 제한되어 있으므로 ‘만족도’라고 입력합니다. 그러면 유형 및 설명(L) 버튼이 나타나는데 그것을 클릭하여 설명에는 [신체만족도]를 입력하고 유형에는 숫자로 입력하였으므로 [숫자]로 설정해 줍니다.
변수목록 칸에 있는 변수 중 계산하기 위한 변수를 가운데 부분에 있는 수식을 가지고 숫자표현식(E) 안에 계산식을 적어 넣습니다. [(키 + 몸무게 + 가슴둘레 + 허리둘레 + 힙둘레) / 5]를 입력합니다. [그림 7.2]처럼 입력하시면 됩니다.
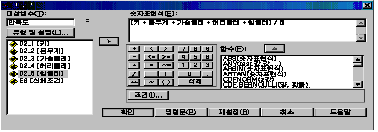
그런 후에 [확인]을 누르면 [그림 7.3]과 같이 데이터 편집기 창에 ‘만족도’라는 변수가 생성됩니다.
그러면 이제부터 신체조건과 만족도라는 변수를 가지고 일원분산분석을 실시하겠습니다. 절차는 다음과 같습니다.
|
분석(A)→평균비교(M)→일원배치 분산분석(O) |
이 절차를 따르면 [그림 7.4]의 대화상자가 나타납니다.
왼쪽 변수 목록 칸에 있는 변수 중에 종속변수인 신체만족도를 종속변수(E)칸에 독립변수인 신체조건을 요인(F)칸에 옮겨놓습니다.
① 대비(C)
대비란 어떤 변수에 의해 케이스들이 여러 개의 집단으로 나누어진 경우, 그 중에서 서로 공통적인 특성이 있는 집단끼리 묶어서 두 가지로 범주화한 후 두 범주의 평균 차이에 대한 T-test를 하는 기능입니다. 만일 변수1과 변수3이 공통적이고 변수2와 변수4가 공통적이라면 이에 대한 대비 식은 다음과 같습니다.
대비에 관한 것을 설정해 주기 위해서는 계수(O)칸에 각 집단에 할당된 처음부터 순서대로 입력한 후 [추가]를 누릅니다. 여기서 주의할 것은 그 입력된 값들의 합이 1이 되어야 한다는 것입니다.
만일 다른 set에서도 범주간 대비를 하고자 하면 [다음(N)] 버튼을 눌러서 같은 방식으로 설정해 주면 됩니다.
② 사후분석(H)
사후분석에서는 Tukey, Duncan, Scheffe 등이 많이 쓰입니다.
Tukey법은 각 셀의 크기가 같은 경우에만 사용합니다. Tukey법은 가장 보수적인 방법입니다. 보수적이란 말은 쉽게 평균에 차이가 유의미하다고 결론 짓지 않는다는 말입니다.
Scheffe법과 Bonferroni법은 각 셀의 크기가 같거나 다르거나 상관없이 사용할 수 있습니다. Scheffe법의 경우 여러개의 대비들을 동시에 검정하는 것에 유효하게 사용할 수 있습니다.
③ 옵션(O)
|
통계량 |
기술통계(D) |
케이스 수, 평균, 표준편차 등의 기술통계량이 출력됩니다. |
|
분산의 동질성(H) |
분산분석을 하기 위해 분산이 동일하다는 가정을 임의로 하게 됩니다. 그러나 표본이 무작위로 추출되었기 때문에 그 가정이 충족되는지 알아보아야 하므로 Levene의 통계량을 이용합니다. | |
|
도표 |
평균도표(M) |
이 분석에 대한 도표가 출력됩니다. |
|
결측값 |
분석별 결측값 제외(A) |
해당 검증과 관련된 변수에 대해 결측값이 있는 케이스를 분석에서 제외시킵니다. |
|
목록별 결측값 제외(L) |
결측값이 있는 케이스는 모든 분석에서 제외시킵니다. |
-->기술통계
신체만족도
|
|
N |
평균 |
표준 편차 |
표준 오차 |
평균에 대한 95% 신뢰구간 |
최소값 |
최대값 | ||||||
|
하한값 |
상한값 | ||||||||||||
|
아주 마른 형 |
1 |
4.2000 |
원글보기 메모 :
'마케팅' 카테고리의 다른 글
| ||||||||||